「20世紀の科学観からの離昇」より
「現代数学」2013年4月号（現代数学社）, 二宮暁（ペンネーム）
フルヴィッツとミンコフスキーが強く後押ししたことでヒルベルトは1900年国際数学会で「数学の問題」として講演を行い，20世紀の数学の夜明けを飾りました．1902年には畏友ミンコフスキーをゲッティンゲン大学に呼び寄せ，彼ら自身の20世紀の数学も始まりました．残念ながらそれは物理にも精通していたミンコフスキーが1909年に48歳の若さでこの世を去ったために完成することはありませんでしたが，ヒルベルトはその遺志を継ぎ，そしてその遺志の中でクーランにより20世紀の科学の礎としての数学書「クーラン・ヒルベルト」［1］が生まれました．
それは数学が全科学の言葉として成熟してゆくという
ヒルベルトとミンコフスキーが夢見ていたものの一つの具現化と考えることができます．
21 世紀を迎えるにあたってアティアらを中心とした国際数学連合はヒルベルトの「数学の問題」の21世紀版［2］を出版しました．しかし，それはヒルベルトが行なったような同一人物による数学全体を俯瞰したものではなく，複数の著者によるものとなりました．20世紀に科学が細分化した事の表れのひとつとみることができます．
20世紀以降，科学者の多くは数学者も含め，一つの専門分野の中で学生時代から定年まで過ごすこととなりました．それらに対応して，20世紀には科学観も大きな変貌を遂げました．
ポパーは「科学的発見の論理」において反証主義を提唱し［3］，クーンは「科学革命の構造」においてパラダイムという考え方を提示しました［4］．
クーンはポパーの反証主義が主張する「科学は反証されることで鍛えられ，反証に耐えられなくなった際に新たな科学にとって代わられる」という現象が科学の歴史の中で主たるものでなかったとしてパラダイム論を提唱したのです．
パラダイムとは科学者（専門家）集団の暗黙の合意事項のことです．
各科学分野には同じ言葉を使いながらもアド・ホックな前提や一種のタブーが存在します．
例えば，同じ電子という言葉を利用しても，電気屋の電子と素粒子論屋の電子は全く異なった様相を持ち，利用される数学の分野も全く異なります．そのため専門家間の意思疎通は原理的に不可能であるという主張がパラダイム論の立場です．共役（通訳）不可能性と呼ばれる問題です．
また，量子力学を想定しても，しなくても，マクスウェルが示したように真理は力学のような決定論的なものとは限らない事も20世紀の科学の大きな知見です．つまり，統計力学などの自然科学の真理は確率論という「起ってみなければ確実なことは判らない」法則に支配されているという事でした．
更には，要素還元主義的な世界観も一部崩壊しました．例えば，アーノルドとマースデンは，1970年前後に理想流体の数学的本質が同時性というものに支配されていることを示しましたが，それは流体力学では同時性を原理とするニュートン力学が，同時性の存在自身を問う相対論的議論よりも本質である事を意味します．流体力学で記述される多くの物理現象においては，相対論的な視点や量子力学的な視点は意味をなくしている事を示しています．
これらの事より科学観は力学を中心とした要素還元主義的な19世紀の科学観（左図）から，20世紀を経てパッチワークのように多様な個々の科学分野がネットワークをなしている科学観（右図）に変化していったと考えるべきです．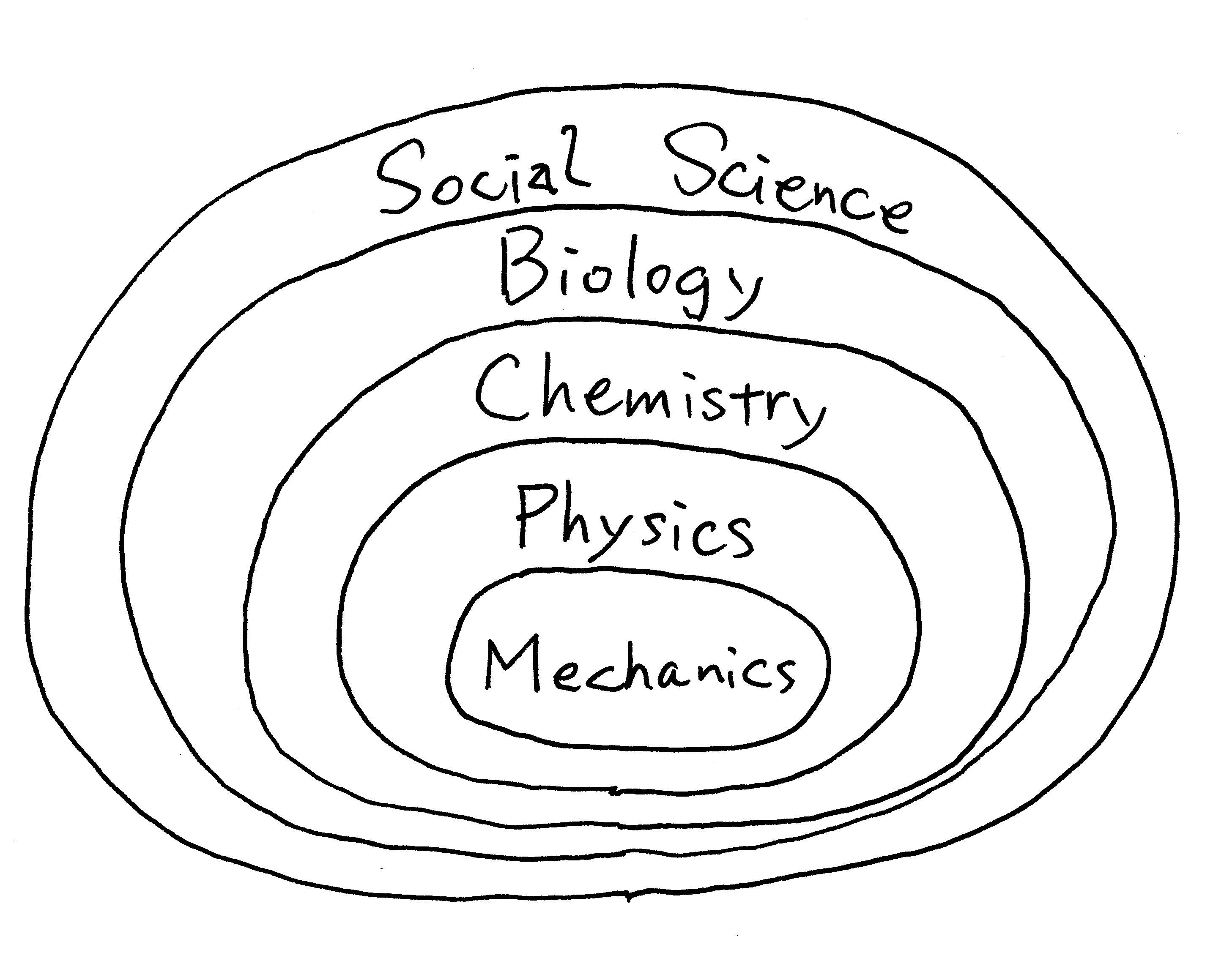
3.11において顕著となりましたが，近年，共役不可能性を根源として，科学の各専門分野が十分連携できず，複雑化した科学技術に対応しきれていない様が顕在化してきているように感じます．賛否の分かれる地球温暖化，遺伝子組み換え食品，リサイクルやバイオ燃料の効能等々がそうです．
それらにおいて社会が科学に求めるものは，科学全体の統一した視点から明
確となっている事実と不明な事実とを，前提条件と共に，列挙することであると思われますが，それが成されているとはいえません．
ポパーは反証という行為によって磨き上げられるのが科学であるとし，科学分野間の意思疎通の障害である共約不可能性は乗り越えられると主張します．クーンはこれに否定的ですが，それでも社会の要求はこの共役不可能性の克服であると言えます．
現代数学においては，幾何学的対象を小さな領域に分解して，それぞれの地図を作成しそれらの重なりを厳密に対応させ，繋がりをもった地図で世界を覆い尽くせば全体像が見えるという考え方を示します．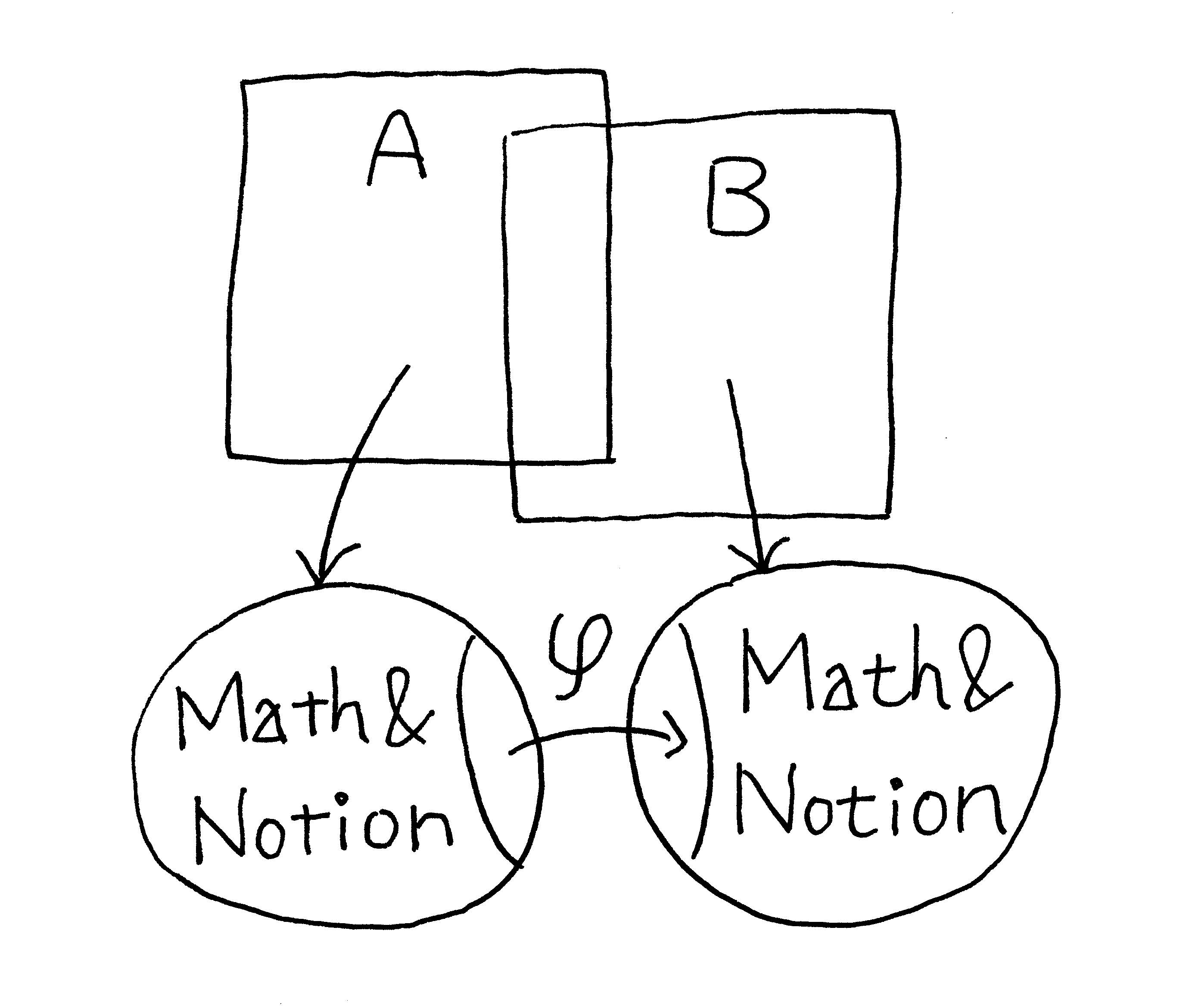
20世紀に発展し成功した概念です．位相幾何，代数幾何，微分幾何，数論幾何では対象の局所的な情報を明確化し，それぞれの繋がりを検討し貼り合わせることで大局的な全体像を得ます．
数学を科学の言葉であると位置づけると科学の専門分野においてそれぞれの対象とする現象は数学で記述され，パラダイムの規約や規範は概念（Notion）として提示されます．電子をディラック方程式の解と見るのか，電子を古典力学の荷電粒子と見るのかということで，異なる数学で記述されます．
つまり，パラダイムは「数学と概念」によって表現されます． それぞれの諸科学の分野を数学という地図で記述し，それらの繋がりを明確化すれば，共役不可能性を克服できるかもしれません．もちろん，数学自身も分化し，細分化され，微分幾何と代数幾何の間でさえもその意思疎通は難しくなっているように感じます．
それでも，数学の厳密性のため共役不可能性を克服することが期待できます．
21世紀の科学に求められるもののひとつは科学者や技術者が長年アドホックの仮定としていたものを明確にし，異なるパラダイムの間の連結部を少しでも強化してゆくことであると思います．その際，数学は重要な役割を果たす責務があると思われます．
これは対象を高次元の平坦な空間に埋め込んで考えるのではなく，部分に分解して考察する方法です．
つまり，科学全体を記述できる新たな「クーラン・ヒルベルト」を用意するのではなく，パラダイム個々に数学の言葉を用意して，各パラダイムの間を通訳してゆくことを目指すのです． それにより科学全体として，自然現象，社会現象を俯瞰し，理解することに繋げてゆくわけです．
つまり，この科学全体の地図を作ってゆく際，言葉としての役割が21 世紀の数学にはあると考えています．
この作業はメルカトルの手法というより地を足で歩き，分解できる地図によって日本地図を構成した伊能忠敬のやり方を想起させます． それはとても地道なものです．
1800年，忠敬は56歳になった後に16年をかけて測量のため各地を歩き，死後,1821年に日本地図を完成させました． 忠敬の示したことは， 地を這うことで，大気圏外から眺
めた姿を想念し，進むべき道を思慮することが重要ということであると感じます．
高みから俯瞰することを想念しながらも，大地に立った21世紀の数学像を示して行きたいと思います．
【参考文献】
［1］ R. Courant, D. Hilbert, Methoden Der Mathematischen Physik, 1924年
［2］ Mathematics : Frontiers and Perspectives, AMS, 2000.
［3］ K. Popper, The Logic of Scientic Discovery（Routledge Classics）, Routledge, 2nd ed. 2002
［4］ T. クーン（中山茂訳） 「科学革命の構造」 みすず書房 1971年