「いまこそ理系よ 立ち上がれ!」より
「理系への数学」2011年7月号(現代数学社), 二宮暁(ペンネーム)
こんなときに「再生への数学:いまこそ理系よ 立
ち上がれ!」というタイトルもないだろうと思わなく
もありません.しかし,こんなときだからこそ「再生
への数学:いまこそ理系よ 立ち上がれ!」だとも思
うのです.
先月号掲載の『東北地方太平洋沖地震に向けて』に
もありましたが,被災地の悲惨な現状は言葉になら
ない悲しい思いと共に,自然災害の驚異と,科学技
術の脆弱性と,科学技術と日常生活との近すぎる距
離とを教えてくれました.それらの事実を前に「自分
は何ができるのか」,「本来どうすべきだったのか,そ
してこれからどうするべきなのか」と考えた人がたく
さんいるように思います.
だからこそ「再生への数学:いまこそ理系よ 立ち
上がれ!」なのです.
人類は様々な災害を乗り越えてきました.乗り越
えるために英知を結集し,知恵を次世代に残してき
ました.測量学と幾何学はナイル川の氾濫のために
発展しました.科学と科学技術はそのような様々な
困難を経て発展してきたのです.
最新の技術は最新の概念の上に築かれています.
更には利害が拮抗する様々な様相が存在し,その関
係は絡み合っています.新たな概念を理解し,その
数値や一見相反する事実から現実の状態を読み取る
事が必要となります.科学技術は数学を言語として
いるのですから,限界はあるにしても数学を操るこ
とで,世界を読み取ることが求められています.
その意味で数学が担う役割には大きなものがあり
ます.次世代に向けて数学により現状を表現し,英
知を伝える責務があると感じます.また,数学が少
しでも判る人には,数学を全く判らない人々に向け
て,現状を判り易く伝えるという責務もあると思い
ます.それが理系のすべき事です.
だからこそ「再生への数学:いまこそ理系よ 立ち
上がれ!」なのです.
理系の人間が現状を理解し,それを判断する.原
子力発電の推進であろうが反対であろうが,数値を
出して議論をして,数値として結論を出す.今回の
福島の原子力発電所の事故が,民主主義国家の中で
起きた事実は重要です.東京電力や政府の批判だけ
ではなく,理系である我々は負った責務に従い,現
実と対峙してきたのかが問われていると思います.
原子力発電による恩恵を受けていたにも関わらず,
安全地帯に身をおいて批判を繰り返しても何も始ま
りません.ヒステリックになる事なく物理現象や数
理現象や工学現象や社会科学現象として,数式やグ
ラフ,数値を利用して理解し,判断すべきなのです.
更には,現在,進行している様々な他の課題の中
に,同種のものはないのかと探ることも重要です.
そのように考えたときに,情報があまりに足りな
いのも事実です.情緒的なものや,単なる結果では
なく,理系の世界を読み解くに足るだけの情報が必
要です.ところが文系的フィルタがかかっているよ
うに思うのです.つまり,理系的な視点が成熟して
いないのです.政府機関や報道機関から事実を十分
に把握するための情報が提供されていません.
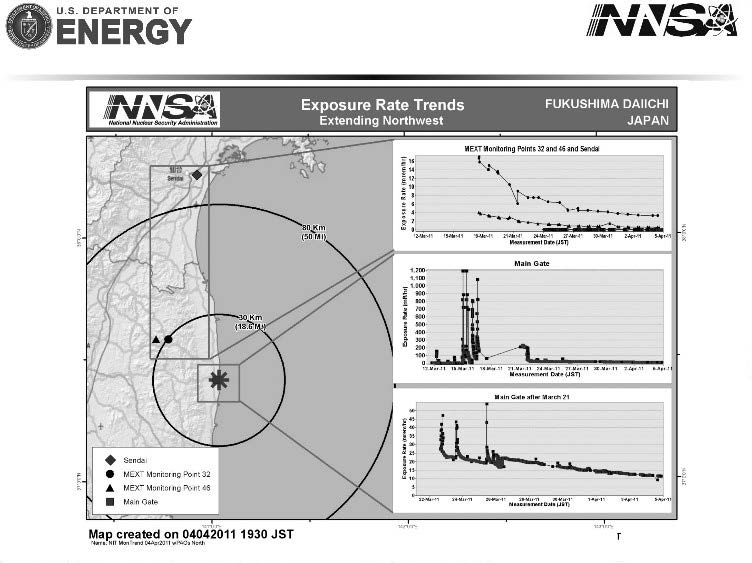
ここで情報の提供の不十分さは情報の隠蔽という
事を単に意味しているのではありません.例えば,
図(http://www.energy.gov/news/10194.htm)は今回の震災に関する米国のエネルギー省のレポ
ートの一頁です.図の下の2 つのグラフは日本から
発せられた情報を基にしていると思われますが,日
本のどの報道機関や政府機関の説明より判り易く理
系的です.単なる当日のデータの発表のみではなく
過去からの時系列データをグラフ化し,それ以外も
理系であれば読み解けるデータが提供されています.
また,1999 年の東海村のJCO での原子力事故で
も同様な事を感じました.この事故では臨界に達す
ることで放射線が放出され周辺住民を含む667 名の
方が被爆しました.周辺住民は臨界に達した時から
臨界の終結までの20 時間にJCO から放出された中
性子線等の放射線によって被爆したようです.
様々な障害物や地形に依存するとは言え,中性子
などの放射線の放出はガウスの法則に従い,もっと
いうと質量の保存から,その量は半径をR とすると
1/R2 に比例します.飛翔の途中での放射線の減衰
を考えなければ,球の表面積4rR2 に従って薄まっ
てゆくからです.しかしながら,その当時,私の知
る限りどの報道機関においても,自分の被爆量をそ
の時に居た場所と臨界転換試験棟からの距離R に
よって換算できるという事を述べたものは見あたり
ませんでした.命に関わることなのに,R2 に反比例
するという事実すら共有できないのです.その代わ
りに○○町は大丈夫であるが,△△町は危険である
と報道されました.文系的フィルターと言っている
のはこの事です.もちろん,町名を挙げることは重
要です.しかしそれのみというのが問題なのです.
2009 年の新型インフルエンザ禍の時も同様です.
必ずしも,米国の判断が正しいとは思いませんが,
アメリカ疾病予防管理センター(CDC)の提供する情
報は,日本の様々な機関が提供した情報より,科学
的でかつ具体的でした.
我々は理系の文化を構築し,それを標準化し,そ
の標準にあわせたデータを要求,抽出させ,それに
より,世界を読み解かなければなりません.その時
にベースとなる数学の役割は大きくなるはずです.
もちろん,その道のりは遠いと考えています.それ
でも,20 年後くらいを目標にすれば,必ずしも不可
能とは断言できないと考えています.
ヒルベルトは19 世紀末の数学の混乱を前に1900
年に第2 回国際数学者会議において「数学の将来の
問題について」と題して,数学の再構築を目指した
講演を行いました.それから,様々なものが軌道に
乗り始めるのに20 年くらいの時間が必要であった
ようです.実際,数学の基礎を片付けた後には物理
学を,というヒルベルトの意志を汲んで,その弟子
クーラントが物理学の基礎としての数学書「クーラ
ン・ヒルベルト」[1]を完成させたのは1924 年です.

もちろん, 目
標に向けては数学
自身も幾つかは変
わってゆかなけれ
ばならないと考え
ています. それ
は, 決して日本
だけの問題ではな
く,世界的な問題
です.また数学だ
けではなく,基礎
科学全体の問題か
もしれれません.
数学を含め基礎科学にある種の行き詰りがあるよう
です.フォン・ノイマンは「数学は経験に即したその
発生の原点から遠く離れ,「現実」から乖離した第二,
第三世代になると,致命的な危機に陥ります.……
危機とは摩擦を避けた安直な発展であり,原点を忘
れることによる学問の無意味な分岐であり,瑣末な
精密化や複雑化を意味します.」[2 ](著者訳)と書き
ました.現状をどう捉えるかは議論が必要ですが,
それでも,この言葉は重いと思います.
ヒルベルトが論じた頃より,21 世紀は数学が科学
技術の基礎として深く生活に入り込んでいます.世
界が複雑化した中で数学に何ができるのか.今こそ
物理に限らず,全科学,工学に向けた21 世紀版の
「クーラン・ヒルベルト」の構築を目指すときです.
再生に向けて数学はどうあるべきか,どのように
考えるべきかというような事を少しづつ書いてゆく
ことにします.
参考文献
[1] R. Courant, D. Hilbert Methoden Der Mathematischen
Physik 1924
[2] J. von Neumann, The Mathematician, The Works
of the Mind edited by R. B. Heywood, Univ. Chicago
Press 1947